Définitions

Utilité

Intuitivement, on perçoit le plus souvent la notion de décision comme un choix entre plusieurs alternatives, effectué en fonction de l'utilité de chacune (rationalité). La notion d'utilité est centrale dans plusieurs contextes, dans la mesure ou une chose utile acquiert une valeur en fonction de la finalité qui lui échoit. Le terme utilité peut donc désigner la valeur d'usage d'un bien – sa capacité à satisfaire un besoin ou un désir (économie).

Mathématiquement, l’utilité est un concept ordinal. Ainsi par exemple, une fonction d’utilité peut représenter la façon dont on attribue une valeur à différents paniers de consommation : les paniers les plus désirables reçoivent des valeurs d'utilité supérieures à celles des paniers qui le sont moins. En d’autre termes, un panier formé des biens (x1,x2) est préféré à un panier formé des biens (y1,y2) si et seulement si le niveau d’utilité de (x1,x2) est supérieur a celui de (y1,y2). Ce qui s'écrit : (x1,x2) ≻(y1, y2) iff u (x1,x2) >(y1, y2).

Décision

Mathématiquement, un problème de décision se présente traditionnellement de la manière suivante :

• un ensemble de décisions possibles (cardinal I) :D : {d1 , … , di, …, dI}.

• un ensemble de critères (cardinal J) caractérisant les états possibles pour di :C1 , … , Cj, …, CJ.

• une projection de l’ensemble vectoriel de ces caractéristiques sur l’ensemble des réels IR (d’où une comparaison possible sur des nombres), souvent exprimée à partir d’une fonction de préférence ou d’utilité U : U = f(C1 , … , Cj, …, CJ).

Une fonction d’utilité f(U) représente la façon dont on attribue une valeur à différents objets, qui peuvent être des "paniers" de produits de consommation (X, Y, Z ...). Le résultat produit par l'application d'une fonction d'utilité sur un ensemble d'objets est un classement hiérarchique des objets de cet ensemble (X>Y>Z...). 

Exemple : Soit f(U) une fonction d'utilité qui attribue aux paniers les plus dérirables des valeurs d'utilité supérieures à celles des paniers qui le sont moins.  Autrement dit, un panier formé des biens (x1,x2) est préféré à un panier formé des biens (y1,y2) si et seulement si le niveau d’utilité de (x1,x2) est supérieur a celui de (y1,y2). Ce qui s'écrit : (x1,x2) ≻(y1, y2) iff u (x1,x2) >(y1, y2).

Considérons un panier de référence z. On appelle courbe d’indifférence associée à z l’ensemble I1 qui contient tous les paniers que le consommateur considère équivalents à z.

Choix optimal

Soit trois courbes d’indifférence d’un consommateur (u1, u2, u3) et la droite rr' représentant son budget au regard des biens x1 et x2.

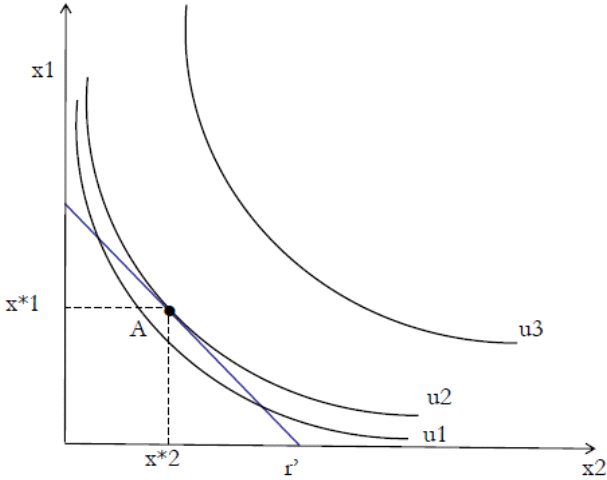
On désire identifier le panier de biens situé sur la courbe d’indifférence la plus élevée

Partons du point r' de la droite de budget et allons vers la gauche

On atteint les courbes d’indifférence u1 puis u2 avec u2>u1

On s'arrête quand on atteint la courbe d’indifférence u2

Sur notre figure ce panier est noté (x1*,x2*)

Le panier (x1*,x2*) constitue le choix optimal du consommateur

L’ensemble des paniers qu’il préfère à (x1*,x2*), n’a pas intersections avec l’ensemble des paniers qui lui sont accessibles (les paniers en dessous de la droite de budget)

Le panier (x1*,x2*) est donc le meilleur panier que le consommateur puisse acquérir

Le panier optimal se situe au point de tangence entre la courbe d’indifférence et la droite de budget

Contextes de décision

L’existence d’une pluralité de combinaisons de critères de choix possibles (coûts-avantages, coûts-efficacité, approches multicritères) est le signe manifeste de la complexité des problèmes de choix.

Par ailleurs les choix d’un individu ont souvent des répercussions sur d’autres individus. Le problème de la décision conduit aussi à introduire les complexités liées aux interdépendances passives entre agents (externalités) et actives (interdépendances stratégiques modélisées par la théorie des jeux).

Le type de décision varie selon un certain nombre d’éléments distinctifs :

- le caractère plus ou moins certain des états futurs de la nature : état certain ou incertain que l’on peut différencier, en utilisant la définition de Knight [1921] en incertitude mesurable (les états ont des probabilités au moins subjectives connues : situation de risque et utilité espérée), et incertitude non mesurable (les états ne peuvent être définis en probabilité : situation d’incertitude selon D. Kreps [1990]) ;

- le caractère unique ou répété de la décision : dans les décisions répétées l’information sur les états de la nature augmente souvent, par apprentissage, (avec pour corollaire une réorientation plus facile de la stratégie : alliances, représailles,…) et les probabilités des états peuvent être révisées selon des approches bayésiennes ;

- le caractère séquentiel ou non de la décision : dans les décisions séquentielles le décideur intervient à différentes étapes, d’où des interactions entre ses décisions successives et une préférence pour la flexibilité, d’autant plus importante que l’information est croissante ;

- le caractère exogène ou endogène de la décision : lorsque l’environnement est exogène le décideur est un preneur d’états (state taker), contraint à des stratégies adaptatives ; en revanche dans un environnement endogène, il peut modifier les états qui deviennent contingents à sa décision, ainsi que les probabilités de leur occurrence ;

- le caractère partagé ou non de la décision : dans le cas de la décision considérée comme un acte collectif, se posent deux problèmes difficiles : la définition d’une fonction d’utilité commune

agrégeant les préférences individuelles des agents, les modalités pratiques d’émergence d’une solution collective efficiente ;

- le caractère conflictuel ou non de la décision : on distingue les jeux contre la nature (absence de conflit car la nature ne nous veut ni du bien ni du mal) et les jeux véritables entre joueurs différents qui sont en situation d’interdépendance stratégique (R. Selten [1988, 1991]).

A cette diversité de contextes, correspondent de multiples méthodes et critères de décision.

On trouvera ci après un exemple de recherche opérationnelle d'une combinaison optimale de choix. On trouvera également sur ce site :

- 2 exemples de processus de décision multicritères (classement des stratégies de gestion des collectivité territoriales (GESTIONSCC et GESTIONSCOM)) :

https://educator6.webnode.fr/decidons/gestionscc

https://educator6.webnode.fr/decidons/gestionscom.

- un exemple de processus de prise de décision stratégique individuel (CAMARApli):

https://educator6.webnode.fr/decidons/applications/

https://prospector0.webnode.fr/camar-competitiveness-of-agriculture-and-management-/en-anglais/ :

...

- et sur le site "prospector", plusieurs exemples de processus de prise de décision multi-agents qui implémentent le concept d'utilité espérée (négociation collaborative (SPRITE et ECOFOR) :

prospector0.webnode.fr/sprite/

prospector0.webnode.fr/sprite/en-anglais/

prospector0.webnode.fr/sprite/irish-case/

cms.prospector0.webnode.fr/ecofor-%28ecologie-foresti%C3%A8re%29/

Exemple de recherche d'une combinaison optimale de plusieurs choix

La Recherche Opérationnelle est une discipline scientifique qui s’intéresse à la compréhension et à la résolution de problèmes de décision. C'est une démarche d'investigation et de planification basée sur la modélisation mathématique du processus de décision afin de déterminer les valeurs des variables qui maximisent / minimisent la valeur d'une équation – combinaison linéaire de ces variables nommée « fonction objectif », tout en vérifiant simultanément un système d’inéquations linéaires mobilisant ces mêmes variables – nommées « contraintes ».

Formulation mathématique

Le problème a été formulé ainsi par Fourier (1768-1830) puis Dantzig (1947):

Notations :

Z est la fonction objectif dont la valeur est à maximiser (évaluation de la décision)

Xj : (j varie de 1à n) sont les variables de décision dont les valeurs sont à déterminer -- ce sur quoi porte la décision, mais aussi ce qui permet d’exprimer les contraintes

Cj sont les coefficients des variables dans la fonction économique. Ce sont les contributions unitaires de chaque variable au niveau de la fonction économique.

aij : sont les coefficients des variables dans les contraintes (i varie de 1 à k et j varie de 1 à n). Ce sont les coefficients techniques , c‘est le nombre d‘unités requises de la ressource i pour réaliser une unités d‘activité j

bi : sont les coefficients du second membre des contraintes. Ce sont, par exemple, les « ressources » disponibles.

Exemple (cas d'école):

Un épicier souhaite vendre 60 citrons et 110 oranges sous la forme de 2 types de lots de fruits : un lot A qui comprend 5 citrons et 1 orange à 4 €, et un lot B qui comprend 1 citons et 10 oranges à 6 €. Combien doit-il proposer de lots A et de lots B pour que sa recette soit maximum ?.

Formulation du problème :

Si on désigne par x1 le nombre de lot A et par x2 le nombre de lot B, le problème revient à chercher le couple (x1, x2) qui maximise la valeur de l'équation y=4x1+6x2 tout en vérifiant le système d'inéquations linéaires suivant :

x1>=0

x2>=0

5x1 +x2 <= 60

x1 +10x2 <= 110

Représentation graphique du problème et de sa solution

Définissons un plan orthonormé x1 (abscisses), x2 (ordonnées).

Traçons les droites qui représentent les équations suivantes :

x1=0 définit l'axe des abscisses et les valeurs mini de x1

x2=0 définit l'axe des ordonnées et les valeurs mini de x2

x2 = - 5x1 + 60 (droite alpha) coupe l'axe des abscisses en C(12,0) et définit les valeurs maxi de x2

x2= - x1+11 (droite beta) coupe l'axe des ordonnées au point A(0,11) et définit les valeurs maxi de x1

Les droites alpha et beta se coupent au point B(10,10)

x2=-2/3x1 – droite S qui représente la valeur mini (0) de fonction à maximiser.

La valeur de y=4x1+6x2 croît lorsque croissent les valeurs de x1 et x2, i.e. au fur et à mesure de la translation affine de la droite S (x2=-2/3x1 ) du point O au point B. Lorsque S est au point O (x1=0 ; x2=0) y=0 car on ne vend rien. Lorsque S est au point C (x1=12 ; x2=0) y=48 € ; les 12 lots A épuisent les 60 citrons mais laissent 98 oranges invendues. Lorsque S est au point A (x1=01 ; x2=11) y=66 €; les 11 lots B épuisent les 110 oranges mais laissent 49 citrons invendus. Lorsque S est au point B (x1=10 ; x2=10) y = 110 € ; en vendant 10 lots A et 10 lots B, on obtient 100 € et il ne reste aucun citron et aucune orange.

.

Techniques de résolution des systèmes d’équations linéaires

Lorsque les systèmes comportent plus de 2 inconnues, la méthode graphique n'est pas utilisable. On procède alors une représentation matricielle du problème et à l'utilisation d'algorithmes de calculs.

On appelle système linéaire à m équations et à n inconnues tout système de la forme suivante :

Les coefficients aij et bi sont des réels donnés, alors que (x1, x2, -----xn) sont les inconnues du système.

La résolution du système revient à déterminer l‘ensemble des solutions (x1, x2, -----xn).

Exemple :

Soit le système d'équations linéaires qui détermine la variation du prix (en euros) d'une poutre (y) au prix d'une dalle (x) :

40y − 20x = 180

50y +10x = 295.

Méthode par substitution

La méthode de résolution d’un système par substitution consiste à exprimer une inconnue en fonction de l’autre, à l’aide de l’une des équations, puis à remplacer dans l’autre équation cette inconnue (substitution) par l’expression obtenue. On a alors une équation avec une seule inconnue, donc facile à résoudre.

À partir de la première équation on obtient y = 0,5x + 4,5. On va alors remplacer, dans la deuxième équation, y, par 0,5x + 4,5. Ce qui nous donne : 50(0,5x + 4,5)+10x = 295. Donc : 35x = 70.On obtient donc : x = 2.

On peut alors calculer y en reprenant la première équation : y = 0,5x + 4,5 = 0,5× 2+ 4,5 = 5,5.

Une poutre coûte donc 2 € et une dalle 5,5 €.

Méthode par combinaison linéaire

La méthode de résolution d’un système par combinaison consiste à multiplier chaque équation par un coefficient bien choisi pour qu’en additionnant (ou soustrayant) les deux équations, l’une des inconnues « s’élimine ». On a alors une équation avec une seule inconnue, donc facile à résoudre.

En multipliant la première équation par 1 (donc on n’y touche pas) et la deuxième par 2, on voit que les termes en x vont s’éliminer si l’on ajoute membre à membre les deux égalités. En effet on a :

40y- 20x= 180 (1)

50y+ 10x= 295 (2)

.

En additionnant les deux égalités membre à membre on obtient :

(40y − 20x )+(100y + 20x ) = 180 + 590.

Soit : 140y = 770. C’est-à-dire : y = 5,5.

On peut alors calculer x avec une des deux équations de départ (ou faire une autre combinaison qui « élimine » l’inconnue y).

Méthode de Gauss ou du pivot

La méthode du pivot de Gauss consiste à transformer un système de m équations linéaires à n inconnues en un système triangulaire équivalent plus simple à résoudre. Cette démarche est basée sur le fait qu‘on ne modifie pas l‘ensemble des solutions d‘un système linéaire lorsqu‘on effectue les transformations élémentaires suivantes : échanger deux équations du système, multiplier une équation par nombre réel non nul, ajouter à une équation le produit d‘une autre équation par un nombre réel.

Si a11 ≠ 0 Pour tout i tel que 2 <= i <= m on procède à l‘opération suivante :

Le terme a11 est nommé « pivot » de l'opération qui élimine l‘inconnue x1 des équations L2, L3-----Lm. On obtient ainsi un système équivalent (S‘). Le système (S‘) est formé de la première équation de (S) et d‘un système de (m-1) équations à (n-1) inconnues. Il reste à trouver un second Pivot et à recommencer le même ensemble d‘opérations.

Exemple :

 Problème primal et problème dual

Dans le problème primal, la fonction objective est une combinaison linéaire de n variables. Il existe m contraintes, chacune d'entre elles plaçant une limite supérieure sur une combinaison linéaire des n variables. L'objectif est de maximiser la valeur de la fonction objective soumise aux contraintes. Une solution est un vecteur (une liste) de n valeurs qui atteint la valeur maximale pour la fonction objective.

Dans le problème dual, la fonction objective est une combinaison linéaire des m valeurs qui sont les limites des m contraintes du problème primal. Il existe n contraintes duales, chacune d'entre elles plaçant une borne inférieure sur une combinaison linéaire de m variables duales.

Relation entre le problème primal et le problème dual

Dans le cas linéaire, dans le problème primal, à partir de chaque point sous-optimal qui satisfait toutes les contraintes, il existe une direction ou un sous-espace de directions vers lesquelles se déplacer, ce qui augmente la fonction objective. On dit que le déplacement dans une telle direction supprime l'écart entre la solution candidate et une ou plusieurs contraintes. Une valeur irréalisable de la solution candidate est une valeur qui dépasse une ou plusieurs contraintes.

Dans le problème dual, le vecteur dual multiplie les contraintes qui déterminent les positions des contraintes dans le problème primal. Faire varier le vecteur dual dans le problème dual équivaut à réviser les bornes supérieures dans le problème primal. La borne supérieure la plus basse est recherchée. Autrement dit, le vecteur dual est minimisé afin de supprimer l'écart entre les positions candidates des contraintes et l'optimum réel. Une valeur irréalisable du vecteur dual est une valeur trop basse. Elle définit les positions candidates d'une ou plusieurs des contraintes dans une position qui exclut l'optimumm réel.

Un exemple concret est donné dans la recherche des conditions d'optimisation des stratégies des exploitations agricoles face à la PAC (CAMAR Appli). decidons/applications/