Economie régionale
Ce document rapporte un exemple d'application de certaines propriétés de l'algèbre des ensembles (indiscernabilité, réduction, régions limites, appriximation) pour analyser les variations dans l'espace de la valeur du rapport entre les emplois des activités économiques basiques d'un territoire (i.e. celles qui visent la satisfaction d'une demande externe au territoire : agriculture, industrie, tourisme, ...) et l'emploi total -- rapport nommé "coefficient multiplicateur".
Problème
Un ensemble U = {… , x, y, … .} comprenant 362 études indique que le rapport entre les emplois des activités économiques basiques d'un territoire (i.e. celles qui visent la satisfaction d'une demande externe au territoire : agriculture, industrie, tourisme, ...) et l'emploi total -- rapport nommé "coefficient multiplicateur", varie beaucoup dans l'espace et dans le temps.
Chaque région est décrite par un ensemble fini de 10 attributs A {X1, X2, X3, R1, R2, R3, R4, R5, R6 L} considérés comme les déterminants potentiels de la valeur de l'attributs D (estimateur du «coefficient multiplicateur de la base ») calculé dans chaque région lors de chaque étude.
X1 = Nombre d’habitants de la zone étudié
X2 = Pourcentage d’emplois dans le secteur primaire
X3 = Pourcentage d’emplois dans le secteur tertiaire
R1 = Délimitation de la zone d’étude (1 = administratif ; 0 = géographique)
R2 = Spécification du modèle de calcul de la base (1 = ratio ; 0 = autre)
R3 = Type de multiplicateur (1 = emplois ; 0 = revenus)
R4 = Mode de détermination des activités basiques : coefficient de localisation (1 = oui ; 0 = non)
R5 = Mode de détermination des activités basiques : utilisation du besoin minimal (1 = oui ; 0 = non)
R6 = Mode de détermination des activités basiques : méthode d’affectation (1 = oui ; 0 = non)
L = Contexte géographique de la zone d’étude (1 = Amérique du Nord ; 0 = Europe).
La valeur des attributs est décrite par un nombre entier qui représente le numéro d'ordre de la classe de valeur à laquelle appartient la valeur exacte de l'attribut (soit {0,1,2,3,4} pour X1,X2, X3 et D ; {0,1} pour les autres attributs).
Quelles sont les explications les plus probabbles des variation de valeur de D? .
Méthode
Lorsque dans un ensemble d'objets U = {… , x, y, … .} -- dans lequel chaque objet est décrit par un ensemble fini d'attributs A {a,b,c,d} dont la valeur est décrite par une nombre entier appartenant à un ensemble fini C qui représentent le numéro d'ordre de la classe de valeur à laquelle appartient la valeur exacte des attributs, deux objets x, y ∊ U sont décrits par un ensemble d’attributs A' ∊ A (exemple A' = {a,b}) de même valeur, ces deux objets x, y sont qualifiés d’indiscernables du point de vue A'.
Les ensembles d’objets indiscernables { B } permettent de décrire avec certitude certaines des relations qui existent entre la variable dépendante D et ses déterminants potentiels X1...L , sous la forme de relations du type : « Si les conditions C (C = liste de valeurs des déterminants potentiels de la variable dépendante observées dans { B }) sont réunies, alors la variable dépendante prend la valeur D (classe de valeur du multiplicateur observée dans { B }) ».
Les ensembles d’objets discernables { A } sont qualifiés d’« ensembles approximatifs » en raison du caractère imprécis des relations qui existent entre la variable dépendante et ses déterminants au sein de ces ensembles. Tout ensemble approximatif { A } peut être décrit par une paire d’ensembles élémentaires { B- } et { B+ }, respectivement appelés « ensemble de plus faible approximation » de {A} et « ensemble de plus haute approximation » de { A }.
L’ensemble de plus faible approximation d’une classe de valeur de la variable dépendante D comprend les objets qu’il est possible de classer dans l’ensemble { A } avec certitude, en raison des relations observées entre la variable dépendante D et ses déterminants potentiels (X1..L). L’ensemble de plus haute approximation comprend les objets qu’il serait possible de classer dans l’ensemble { A } en raison de la valeur prise par certains déterminants (i.e. parce que X1 et ou X2 .. ou L ont une valeur similaire à celle observées dans l’ensemble { B- }), mais qui ont d’autres propriétés qui ne sont pas observées dans l’ensemble { B- }.
Il résulte de cette définition que les objets qui ne peuvent être classés dans l’ensemble de plus haute approximation { B+ } n’appartiennent assurément pas à l’ensemble { A }. Cet ensemble d’objets permet de décrire les autres relations qui existent entre la variable décisionnelle et ses déterminants, et d’associer un coefficient de (in)certitude à ces relations. Ce faisant, l’analyse des ensembles approximatifs permet de transformer la base de données en relations entre la variable dépendante D et ses déterminants (X1.. L), et d'identifier les déterminants potentiels non significatifs ainsi que l’influence de chaque facteur déterminant sur la valeur de la variable dépendante
Résultats
Le SIAD BASECO construit pour mettre en œuvre cette méthode repartit les 362 études resensees dans la littérature en 4 ensembles principaux (El, E2, E3, et E4), en fonction de leur contribution à l’estimation de la valeur du multiplicateur (Tableau 1) :

Tableau 1 - Répartition des régions en fonction de leur contribution à l’estimation du multiplicateur
L'ensemble « E1 » rassemble les études où tous les déterminants utilisés (X1, ...L) permettent de statuer avec certitude sur l’appartenance de la valeur du multiplicateur D à une de ses classes de valeurs possibles Cd{0,1,2,3,4} . Cet ensemble définit l’espace des approximations positives les plus faibles du multiplicateur. Il comprend autant de sous – ensembles que de classes de valeurs de la variable dépendante (5). Le rapport entre le nombre d’éléments de ces sous - ensembles et l’effectif total de la classe (nombre d’études où le multiplicateur a effectivement une valeur qui appartient à cette classe) fournit une indication sur la sensibilité de ce type d’approximation aux variations de valeur de la variable dépendante. On notera que l’approximation positive du multiplicateur est rare (difficile) lorsque sa valeur est très faible.
L'ensemble « E2 » rassemble les études où certains déterminants seulement permettent de statuer avec certitude sur l’appartenance de la valeur du multiplicateur à une des classes de valeurs possibles. Cet ensemble définit l’espace des approximations positives les plus fortes du multiplicateur. Il inclut l’ensemble précédent.
L'ensemble « E3 » rassemble les études où tous les déterminants utilisés ne permettent pas de statuer avec certitude sur la classe de valeur du multiplicateur, i.e. les situations où l’on peut conclure à des valeurs différentes du multiplicateur, selon les déterminants auxquels on se réfère. Cet ensemble est le complément de l’ensemble « E1 » dans l’ensemble « E2 ». Il définit la frontière (région « limite ») des approximations possibles de la valeur du multiplicateur, qui sont réalisables à partir des connaissances collectées.
L'ensemble « E4 » rassemble les études où les déterminants utilisés permettent de statuer avec certitude sur la non - appartenance de la valeur du multiplicateur à une classe de valeurs donnée. Cet ensemble définit l’espace des approximations négatives du multiplicateur. Il comprend autant de sous – ensembles que de classes de valeurs de la variable dépendante (5). Le rapport entre le nombre d’éléments de chacun de ces sous - ensembles et l’effectif total de la classe fournit une indication sur la spécificité de chaque classe de valeur du multiplicateur aux études qui sont classées dans chacun de ces sous – ensembles. On notera que la spécificité des classes de valeurs utilisées pour décrire le multiplicateur tend a croître avec la valeur du multiplicateur.
L’analyse des relations qui existent entre la valeur du multiplicateur et celle de ses déterminants dans chacun de ces ensembles et sous–ensembles d’études a permis d’élaborer 121 règles de décision (2).
L’utilisation de ce classifieur--SIAD BASECO--pour déterminer la valeur du multiplicateur à partir de la valeur des déterminants observés dans les 362 régions (qualification), montre que le modèle ainsi construit représente correctement les relations existant entre la [classe de] valeur du coefficient multiplicateur et la [classe de] valeur de ses déterminants dans 78 % des études analysées (Tableau 2).

Tableau 2 - Matrice de confusion de la classification réalisée par le classifieur
Toutefois, ce modèle explique mal les multiplicateurs de très faibles valeurs (inférieurs à 1,485). En effet, la classe 0 est celle pour laquelle la précision (0,43) comme la fiabilité (0,64) sont les plus faibles (tableau 2). La sensibilité et la spécificité prennent aussi les valeurs les plus faibles (0,24 et 0,70 respectivement) pour la classe 0 (tableau 1). De plus, il explique moins bien les coefficients dont la valeur est comprise entre 1,795 et 2,020 (classe 3) que les coefficients dont la valeur est comprise entre 1,485 et 1,795 ou supérieure à 2,020 (Tableau 2). L’explication des valeurs de la classe 3 est effectivement peu précise (0,62). Elle est toutefois relativement fiable (0, 83) puisque sa fiabilité est la seconde la plus élevée.
Les capacités prédictives d'un réseau de neuronnes artificiels (ANNMetaAnalysis_JPB2) construit à partir des mêmes informations ne sont pas meilleures : le taux moyen d'erreurs lors de la phase de prédiction est de 25,4%, car le réseau de neuronnes représente mal les relations entre les données (23,7 % d'erreurs lors de la phase d'apprentissage) ; ce sont les effets de levier des niveaux 0, 2 et 3 qui sont les plus mal modélisés.
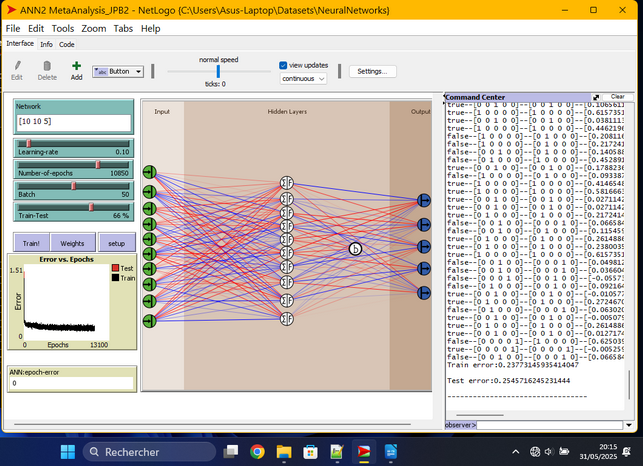
Erreur lors des tests de prédiction :
class4 :5/17
class3 : 4/9
class2 : 21/43
class1 : 10/34
class0 : 12/21
En outre, la construction d'un réseau de neuronnes artificiels n'offre pas les facilités d'analyse des relations modélisées que celles que permet la construction d'un "classifieur".
L’analyse du test de sensibilité des résultats du "classifieur" -- prédictions de la classe de valeur de l'effet de levier -- aux déterminants utilisés pour estimer la valeur du multiplicateur confirme l’influence déterminante du nombre d’habitants de la zone étudiée sur la valeur du coefficient multiplicateur (Tableau 3). En effet, la qualité de la classification est réduite à 0,15 si la variable « population » est supprimée. La forte influence de la population de la zone d’étude (X1log) sur la valeur du coefficient multiplicateur des activités de la base est conforme aux mécanismes économiques en jeu dans le multiplicateur.

Tableau 3 - Influence des déterminants potentiels sur la qualité de l’estimation du multiplicateur

Figure 1. Relations entre les classes de valeurs du multiplicateur et les classes de valeur de la population (X1)
En outre, cette analyse montre que les dix déterminants ne sont pas tous nécessaires pour expliquer la valeur du multiplicateur. Quatre ensembles différents de huit déterminants fournissent des explications de la valeur du multiplicateur de qualités équivalentes : { R3, R2, R4, R6, L, X1, X2, X3 }, { R3, R2, R5, R1, L, X1, X2, X3 }, { R3, R2, R4, R1, L, X1, X2, X3 }, et { R3, R2, R5, R6, L, X1, X2, X3}. Les caractéristiques socio - économiques X1 (population), X2 (emplois du secteur primaire) et X3 (emplois du secteur secondaire), les indicateurs méthodologiques R2 (spécification du modèle de la base) et R3 (type de multiplicateur évalué), ainsi que le contexte géographique L, constituent le tronc commun des quatre explications. En revanche, les indications concernant la délimitation des zones d’étude (R1), l’utilisation de la méthode de localisation (R4), l’utilisation de la méthode du besoin minimal (R5), et l’utilisation de la méthode d’affectation (R6) ne sont pas toutes nécessaires. Si R4 et R6 ou R1 sont spécifiées, alors R5 n’est pas nécessaire. En revanche, si R5 et R6 ou R1 sont spécifiées, alors R4 n’est pas nécessaire.
Les résultats des tests de validation du classifieur (Tableau 4) montrent que ce modèle est relativement stable : 65 % des 356 prédictions réalisées sur des situations exclues de l’échantillon utilisé pour construire le classifieur se sont révélées exactes (Minimum = 0,44, Maximum = 0,65, Écart-type = 0,08) . Mais la stabilité du modèle varie selon la classe de valeur du multiplicateur. Elle est particulièrement faible pour les très petites valeurs du multiplicateur (0,14) (tableau 4). De surcroît, les taux d’erreur sont particulièrement élevés pour ces valeurs (0,75 pour la classe 0 : tableau 4).

Tableau 4 - Résultats des tests de validation du classifieur
La matrice de confusion (Tableau 2) souligne un certain nombre de faiblesses du méta-modèle construit à partir des études collectées. Ainsi, 16 cas dont la classe de valeur observée est 3 ont une valeur prédite de classe 2 (expliquant ainsi la médiocre qualité de la classification de la classe 3). La situation est identique pour 11 cas dont les classes observées et prédites sont différentes (respectivement 2 et 1). Les analyses individuelles de ces cas se révèlent particulièrement pertinentes. Ces 27 cas mal classés correspondent tous à des études où le multiplicateur est exprimé en emplois. Celui-ci est estimé par ratio dans des zones correspondant à un découpage administratif en mobilisant, pour la plupart des travaux, le coefficient de localisation. À l’inverse, les cas bien classés (par exemple les 34 cas de la classe 3) ne cumulent jamais ces quatre choix méthodologiques. Ces résultats confirment les bases théoriques des modèles de la base.
En définitive, les cas mal classés correspondent à des situations où les méthodes pouvant donner potentiellement des résultats médiocres sont employées simultanément : spécification du modèle par ratio (inadaptée pour des économies particulièrement dynamiques), délimitation par découpage administratif et expression du modèle en termes d’emplois (qui ne représentent toujours que des solutions par défaut en raison d’un manque de données), estimation des emplois basiques par coefficient de localisation (inappropriée pour des économies très diversifiées).
Une discussion de ces résultats peut être trouvée dans l'article :
Bousset Jean-Paul, Vollet Dominique, « Apports de l'analyse des ensembles approximatifs à une application de la méta-analyse en économie régionale », Revue d’Économie Régionale & Urbaine 5/ 2003 (décembre), p. 773-798.
On peut également consulter :
Dominique Vollet and Jean-Paul Bousset. Use of meta-analysis for the comparison and transfer of economic base multipliers Vollet, D.§ et al. (2002§) Regional Studies, 36.5 pp 481-494, 2002.
1Une « classe » en statistiques.
2Exemple :
Si le type de découpage géographique est « administratif »
et (si) la zone d’étude est située en Amérique du nord
et (si) la population de la zone est inférieure à 12 650 habitants
et (si) la proportion de la population active employée par le secteur primaire est inférieure à 2,5%
et (si) la proportion de la population active employée par le secteur tertiaire est comprise entre 39 % et 57 %
Alors le multiplicateur de la base est compris entre 1,4 et 1,5.
Si le type de découpage géographique est « administratif »
et (si) la zone d’étude est située en Amérique du nord
et (si) la population de la zone est comprise entre 140 000 et 254 000 habitants
et (si) la proportion de la population active employée par le secteur primaire est comprise entre 2,5 % et 6,5 %
et (si) la proportion de la population active employée par le secteur tertiaire est comprise entre 39 % et 57 %
Alors le multiplicateur de la base est soit inférieur à 1,4, soit compris entre 1,4 et 1,5.